2904. Rook attack
You have been given a rows-by-cols
chessboard, with a list of squares cut out. The list of cutouts will be given.
This problem will involve placing rooks on a chessboard, so that they cannot
attack each other. For a rook to attack a target piece, it must share the same
row or column as the target. Rooks cannot be placed on cut out squares. The cut-out
squares do not affect where the rooks can attack.
Input. Consists of multiple test cases. The first line of
each test case contains three integers: the dimensions of the chessboard rows and
cols (1 ≤ rows, cols
≤ 300) and the number of
cut out squares cuts. Next line gives the list of (x, y)
coordinates of cut out
squares, delimited with a space. The list has a form x1 y1 x2 y2 x3
y3 ... xcuts ycuts.
It is known that 0 ≤ xi ≤ rows – 1, 0
≤ yi ≤ cols – 1.
Output. For each test case print in a separate line the
maximum number of rooks that can be placed on the chessboard, such that no pair
of rooks can attack each other.
|
Sample
input |
Sample output |
|
8 8 0 3 3 6 0 0 1 0 1 1 2 0 2
1 2 2 3 3 3 0 0 1 2 2 2 |
8 2 3 |
SOLUTION
graphs - flows
Algorithm analysis
Let's construct
a bipartite graph. In the first part we'll place rows of vertices, in
the second – cols of vertices. If the cell with coordinates (i, j)
remains uncut on the chessboard, then draw an edge between the i-th
vertex of the first part and the j-th vertex of the second part. The
maximum matching of the resulting bipartite graph is equal to the maximum
number of non-attacking rooks that can be placed on the chessboard. We solve
the problem using the maximum flow, adding two vertices: source and drain.
For example, for
the third test case, the chessboard and the constructed graph will look like:
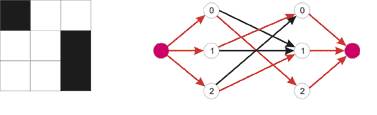
Saturated edges
in the maximum flow are highlighted in red. The flow value is 3, the rooks are
located in cells (0, 2), (1, 0) and (2, 1).
When
constructing the capacity matrix m, the vertices of the graph have the
following numbers:
·
source: number 0;
·
first part: from 1 to rows;
·
second part: from rows
+ 1 to rows + cols;
·
drain: number rows
+ cols + 1;
Example
In the third
test case, cells (0, 0),
(1, 2), (2, 2) are cut out. You can place 3 rooks on the board that do not
attack each other.

Algorithm realization
Declare the global
arrays and variables.
#define MAX 602
int m[MAX][MAX], used[MAX], MaxFlow, flow;
The function aug finds an augmental path from x
to t using depth-first search and returns the value of the maximum flow
in it.
int aug(int x,int t,int CurFlow)
{
if (x == t) return
CurFlow;
if (used[x]++) return
0;
for (int Flow,y = 0;
y < n; y++)
{
if (m[x][y] > 0 && (Flow =
aug(y,t,min(CurFlow,m[x][y]))))
{
m[x][y] -= Flow; m[y][x] += Flow;
return Flow;
}
}
return 0;
}
The function BuildMatrix
constructs a bipartite graph in the adjacency matrix m as described in the
analysis of the algorithm.
void BuildMatrix(void)
{
int i, j, a, b;
Reset the adjacency matrix m. The variable n stores
the number of vertices of the graph.
memset(m,0,sizeof(m));
n = rows + cols + 2;
for(i = 1; i <= rows; i++) m[0][i] = 1;
for(i = 1; i <= cols; i++) m[i+rows][n-1] = 1;
Fill the graph, assuming that there are no holes on the board. Draw an edge
between each vertex of the first and the second part.
for(i = 1; i <= rows; i++)
for(j = 1; j <= cols; j++) m[i][j+rows] = 1;
For each hole with coordinates (a, b) we remove the edge
between vertex a of the first part and vertex b of the second
part.
for(i = 0; i < cuts; i++)
{
scanf("%d %d",&a,&b);
m[a+1][rows+b+1] = 0;
}
}
The main part of the program. Read the input data. Construct
a matrix and run the algorithm for finding the maximum flow.
while(scanf("%d %d %d",&rows,&cols,&cuts)
== 3)
{
BuildMatrix();
MaxFlow = 0;
do
{
memset(used,0,sizeof(used));
} while ((flow = aug(0,n-1,0x7FFFFFFF))
&& (MaxFlow += flow));
printf("%d\n",MaxFlow);
}
Algorithm realization – augmenting path with optimization
#include <cstdio>
#include <vector>
#include <algorithm>
#define MAX 301
using namespace std;
int g[MAX][MAX];
vector<int>
used, par, mt;
int i, j, ptr;
int rows, cols, cuts, a, b, flow;
int dfs(int v)
{
if (used[v]) return
0;
used[v] = 1;
for (int to = 0; to
< cols; to++)
{
if (g[v][to] == 0) continue;
if (mt[to] == -1 || dfs(mt[to]))
{
mt[to] = v;
par[v] = 1;
return 1;
}
}
return 0;
}
void AugmentingPath(void)
{
int i, run;
mt.assign (cols, -1);
par.assign (rows, -1);
for (run = 1; run; )
{
run = 0; used.assign(rows, 0);
for (i = 0; i < rows; i++)
if ((par[i] == -1) && dfs(i))
run = 1;
}
}
int main(void)
{
while(scanf("%d %d
%d",&rows,&cols,&cuts) == 3)
{
for(i = 0; i < rows; i++)
for(j = 0; j < cols; j++) g[i][j] =
1;
for(i = 0; i < cuts; i++)
{
scanf("%d %d",&a,&b);
g[a][b] = 0;
}
AugmentingPath();
for (flow = i = 0; i < cols; i++)
if (mt[i] != -1) flow++;
printf("%d\n",flow);
}
return 0;
}